きりしま屋

で、問題は、オウムガイは黄金比でも白銀比でもないということはどうしてくれよう、ということですね。

画面のタテヨコ比でワイド画面が 16:9 なのが黄金比の近似だというなら、
1:1.3は、そうか、 4:3 のことか（笑）。

従来型の画面のタテヨコ比もある意味、黄金比なのだなあと。

いや、黄金比・白銀比というのなら、

赤銅比か。

あ……書いてる人がいるよ。

二つの比は、名前こそ似ているが、数値的にルールが見出せるだろうか？

ここで登場するのが、連分数である。

　黄金比 [1;1,1,1,…] = (1+√5)/2
　白銀比 [2;2,2,2,…] = 1+√2

と表されるのである。
金、銀ときたら銅だよね。銅と言ったら赤なので、勝手に妄想してみると、

　赤銅比 [3;3,3,3,…] = (3+√13)/2

Doblog - knifeのblog -

連分数からルートに展開するのを学ぶのは面倒だけど、連分数として表わすとこんな感じで、

図：左から黄金比、白銀比、赤銅比（仮）の連分数表現

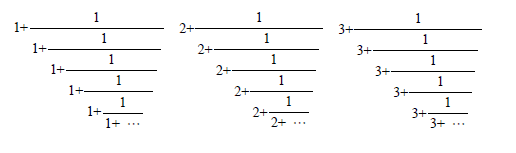
非常に美しいことになっていることが確認でき、しかも、1の黄金比、2の白銀比、3の赤銅比で、オウムガイは赤銅比に近似しているということでスッキリしたので終了。

学問の話ではないので、

タテヨコ比は、

黄金比　1:1.6　だいたい　9:16　か　10:16
白銀比　1:1.4　だいたい　5:7
赤銅比　1:1.3　だいたい　3:4

あたりで構成してみましょう、ということで。

デザインを無理に数学的にこじつけるのではなく、美しい比率を参考にするのであれば、オウムガイの比率が黄金比でなくても、十分に参考にするに値すると、そういうことですな。